Lecture 5: Introduction to Network Analysis¶

Lecturer: Primoz Konda

Course: Natural Language Processing and Network Analysis

Date: 15.10.2024

Agenda for today:¶

What are networks and why do we need them?
Basic structures of relational data
Construction of networks and mesurements
Simple network visualizations
Similarity Graph
Bipartite Graph

Networks¶

Networks are a way of representing interactions among some kind of units:
- In the case of social and economic networks, these units (nodes) are usually individuals or firms.
- The connections between them (links) can represent any of a wide range of relationships: friendship, business relationship, communication channel, etc.

The basic jargon¶

The elements of a a network or graph are commonly referred to as nodes (system theory jargon) or vertices (graph theory jargon) of a graph.
The connections are edges or links.

Types of networks¶

Networks are a form of representing relational data.
This is a very general tool that can be applied to many different types of relationships between all kind of elements.
The content, meaning, and interpretation for sure depends on what elements we display, and which types of relationships. For example:
In Social Network Analysis:
- Nodes represent actors (which can be persons, firms and other socially constructed entities)
- Edges represent relationships between this actors (friendship, interaction, co-affiliation, similarity ect.)
Other types of network
- Chemistry: Interaction between molecules
- Computer Science: The world-wide-web, inter- and intranet topologies
- Biology: Food-web, ant-hives

The possibilities to depict relational data are manifold. For example:

Relations among persons

Kinship: mother of, wife of...
Other role based: boss of, supervisor of...
Affective: likes, trusts...
Interaction: give advice, talks to, retweets...
Affiliation: belong to same clubs, shares same interests...

Relations among organizations

As corporate entities, joint ventures, strategic alliances
Buy from / sell to, leases to, outsources to
Owns shares of, subsidiary of
Via their members (Personnel flows, friendship...)

Relational data-structures¶

Edgelist¶

Common form of storing real-life relational data (eg. in relational databases)
An edgelist is a dataframe that contains a minimum of two columns, one of nodes that are the source of a connection and another that are the target of the connection.
The nodes in the data are typically identified by unique IDs.
If the distinction is not meaningful, the network is undirected (more on that later).
If the distinction between source and target is meaningful, the network is directed.
Can also contain additional columns that describe attributes of the edges such as a magnitude aspect for an edge, meaning the graph is weighted (e.g., number of interactions, strenght of friendship).

In [1]:

import networkx as nx
import matplotlib.pyplot as plt

edgelist = [
    ('Anna', 'Bente'),
    ('Anna', 'Cindy'),
    ('Anna', 'David'),
    ('Anna', 'Ester'),
    ('Anna', 'Frede'),
    ('Ester', 'Frede'),
    ('Frede', 'Gerwin')]

# Create a graph using networkx
G = nx.Graph()
G.add_edges_from(edgelist)




# Plot the graph using Matplotlib
plt.figure(figsize=(3, 3))
nx.draw(G, with_labels=True,
        node_color='red', node_size=1000, font_size=8,
        font_color='white', edge_color='black')

Edgelist:
Anna - Bente
Anna - Cindy
Anna - David
Anna - Ester
Anna - Frede
Ester - Frede
Frede - Gerwin

No description has been provided for this image

In [4]:

# Create the adjacency matrix from the graph
adj_matrix = nx.adjacency_matrix(G).todense()
from IPython.display import display, HTML

# Print "Adjacency Matrix" as a large title using HTML
display(HTML('<h1 style="font-size:24px;">Adjacency Matrix:</h1>'))
# Print the adjacency matrix
print("\n\n\n\n")
print(adj_matrix)

Adjacency Matrix:





[[0 1 1 1 1 1 0]
 [1 0 0 0 0 0 0]
 [1 0 0 0 0 0 0]
 [1 0 0 0 0 0 0]
 [1 0 0 0 0 1 0]
 [1 0 0 0 1 0 1]
 [0 0 0 0 0 1 0]]

In [3]:

# Visualize the adjacency matrix as a heatmap
plt.figure(figsize=(3, 3))
plt.title("Adjacency Matrix Heatmap")
plt.imshow(adj_matrix, cmap='Blues', interpolation='none')
plt.colorbar(label="Edge Weight")
plt.xticks(ticks=range(len(G.nodes())), labels=G.nodes(), rotation=90)
plt.yticks(ticks=range(len(G.nodes())), labels=G.nodes())
plt.show()

Nodelists¶

Edgelists as well as adjacency matrices only stores connectivity pattern between nodes, but due to their structure cannot store informations on the nodes in which we might be interested.
Therefore, we in many cases also provide a a node list with these informations (such as the names of the nodes or any kind of groupings).

id name gender group

 1 Anna       F        A
 2 Bente      F        B
 6 Cindy      F        A
 7 David      M        B
 8 Ester      F        B
 9 Frede      M        A
10 Gerwin     M        B

Graph Objects - Difference between Tabular and Graph data¶

Tabular data:

In tabular data, summary statistics of variables are between observations (column-wise) interdependent, meaning changing a value of some observation will change the corresponding variables summary statistics.
Likewise, variable values might be within observation interdependent (row-wise), meaning changing a variable value might change summary statistics of the observation
Otherwise, values are (at least mathematically) independent.

Graph data:

Same holds true, but adittional interdependencies due to the relational structure of the data.
Sepperation between node and edge data, which is interdependent. Removing a node might alos impy the removal of edges, removal of edges changes the characteristics of nodes. In adittion, the relational structure makes that not only true for adjacent nodes and edges, but potentially multiple. Adding/Removing one node/edge could change the characteristics of every single other node/edge.
That is less of a problem for local network characteristics (eg., a node's degree on level 1). However, many node and edge characteristics such.
That's mainly why graph computing is slightly more messy, and need own mathematical tools, and applications from graphical computing (graphical like graph, not like figure)

Network analysis and measures¶

Often, we are interested in ways to summarize the pattern of node connectivity to infer something on their characteristics.

Centralities¶

One of the simplest concepts when computing node level measures is that of centrality, i.e. how central is a node or edge in the graph.
As this definition is inherently vague, a lot of different centrality scores exists that all treat the concept of "central" a bit different.

We in the following well briefly illustrate the idea behind three of the most popular centrality measures, namely:

Degree centrality
Eigenvector centrality
Betweenness centrality

1. Degree centrality¶

The degree centrality is probably the most intuitive measure of a node's importance. It simply counts the number of edges that are adjacent to a node.

Formally, the degree centrality of a node $i$ is the sum of the edges $e_{ij}$ between node $i$ and other nodes $j$ in a network with $n$ total nodes:

$$ c^{dgr}_{i} = \sum\limits_{j=1}^{n} e_{ij} \quad \text{where} \quad i \neq j $$

In this formula:

$c^{dgr}_{i}$ is the degree centrality of node $i$.
$e_{ij}$ is 1 if there is an edge between nodes $i$ and $j$, and 0 otherwise.
The sum counts the number of edges connected to node $i$, excluding itself (i.e., $i \neq j$).

2. Eigenvector centrality¶

Eigenvector centrality takes the idea of characterizing nodes by their importance in a network further.
The basic idea is to weight a node's degree centrality by the centrality of the nodes adjacent to it (and their centrality in turn by their centrality).
The eigenvector here is just a clever mathematical trick to solve such a recurrent problem.

$$ c^{ev}_{j} = \frac {1}{\lambda} \sum_{t \in M(i)} x_{t} = \frac {1}{\lambda} \sum_{t \in G} a_{i,t} x_{t} $$

In this formula:

$c^{ev}_{j}$ is the eigenvector centrality of node $j$.
$ \lambda $ is the eigenvalue associated with the eigenvector centrality.
$M(i)$ is the set of neighbors of node $i$.
$a_{i,t}$ represents the adjacency matrix element between nodes $i$ and $t$. It's 1 if there is an edge between them and 0 otherwise.
$x_t$ is the eigenvector centrality of node $t$ (a neighbor of $i$).

The eigenvector centrality assigns relative scores to all nodes in the network based on the concept that connections to high-scoring nodes contribute more to the score of a given node than equal connections to low-scoring nodes.

3. Betweenness centrality¶

The betweenness centrality of a node measures the extent to which it lies on short paths.
A higher betweenness indicates that it lies on more short paths and hence should somehow be important for traversing between different parts of a network
How many pairs of individuals would have to go through you in order to reach one another in the minimum number of hops?

Betweenness centrality

$$ c^{btw}_{j} = \sum_{s,t \in G} \frac{ \Psi_{s,t}(i) }{\Psi_{s,t}} $$

where vertices (s,t,i) are all different from each other

$\Psi\_{s,t}$ denotes the number of shortest paths (geodesics) between vertices $s$ and $t$
$\Psi\_{s,t}(i)$ denotes the number of shortest paths (geodesics) between vertices $s$ and $t$ that pass through vertex $i$.
The geodesic betweenness $B_n$ of a network is the mean of $B_n(i)$ over all vertices $i$

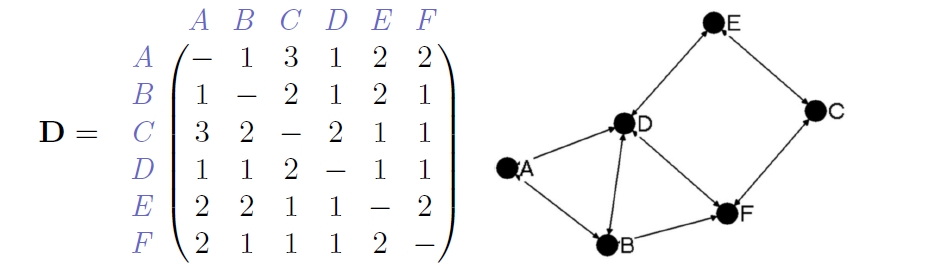
Neighborhood of a Node¶

Lastly, we can look at the surrounding of a node, meaning the ones it is connected to, its neighborhood. Here, we can look at the ego-network of a node. That means how many nodes are in a certain geodesic distance. Plainly speaking, how many nodes are not more than x-steps away.

Clustering (Community detection)¶

Another common operation is to group nodes based on the graph topology, sometimes referred to as community detection based on its commonality in social network analysis.
The main logic: Form groups which have a maximum within-connectivity and a minimum between-connectivity.
Consequently, nodes in the same community should have a higher probability of being connected than nodes from different communities.

Example: The Louvain Algorithm¶

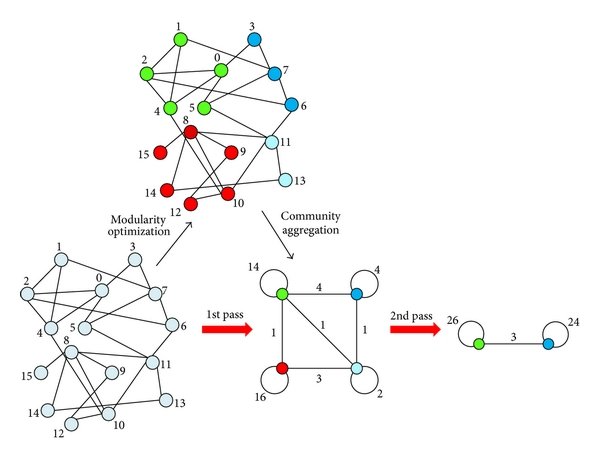
The Louvain Algorithm¶

I will illustrate the idea using the Louvain Method, one of the most widely used community detection algorithms.
It optimises a quantity called modularity:

$$ \sum_{ij} \left(A_{ij} - \lambda P_{ij}\right) \delta(c_i, c_j) $$

$A$ - The adjacency matrix

$P\_{ij}$ - The expected connection between $i$ and $j$.

$\lambda$ - Resolution parameter

Can use lots of different forms for $P\_{ij}$ but the standard one is the so called configuration model:

$$ P\_{ij} = \frac{k_i k_j}{2m} $$

Loosely speaking, in an iterative process it

You take a node and try to aggregate it to one of its neighbours.
You choose the neighbour that maximizes a modularity function.
Once you iterate through all the nodes, you will have merged few nodes together and formed some communities.
This becomes the new input for the algorithm that will treat each community as a node and try to merge them together to create bigger communities.
The algorithm stops when it's not possible to improve modularity any more.

This is the original paper, for those interested in further reads:

Blondel, Vincent D; Guillaume, Jean-Loup; Lambiotte, Renaud; Lefebvre, Etienne (9 October 2008). "Fast unfolding of communities in large networks". Journal of Statistical Mechanics: Theory and Experiment. 2008 (10): P10008

(Global) Network structure¶

Finally, it is often also informative to look at the overal characteristics of the network:

The density of a measure represents the share of all connected to all possible connections in the network
Transistivity, also called the Clustering Cofficient indicates how much the network tends to be locally clustered. That is measured by the share of closed triplets.
The diameter is the longest of the shortest paths between two nodes of the network.
The mean distance, or average path lenght represents the mean of all shortest paths between all nodes. It is a measure of diffusion potential within a network.

Summing up¶

In this session we talked about:

What are networks and why might it be interesting to study them.
What are commong datastructures to represent networks.
What are basic definitions and concepts relevant for network analysis
What are common measures of local network structure?
What are common measures of global network structure?

Network / Graph concepts & terminology¶

The vertices u and v are called the end vertices of the edge (u,v)
If two edges have the same end vertices they are Parallel
An edge of the form (v,v) is a loop
A Graph is simple if it has no parallel edges and loops
A Graph is said to be Empty if it has no edges. Meaning E is empty
A Graph is a Null Graph if it has no vertices. Meaning V and E is empty
Edges are Adjacent if they have a common vertex. Vertices are Adjacent if they have a common edge
Isolated Vertices are vertices with degree 1.
A Graph is Complete if its edge set contains every possible edge between ALL of the vertices
A Walk in a GraphG = (V,E) is a finite, alternating sequence of the form ViEiViEi consisting of vertices and edges of the graph G
A Walk is Open if the initial and final vertices are different. A Walk is Closed if the initial and final vertices are the same
A Walk is a Path if ANY vertex is appear atmost once (Except for a closed walk)