Into Graph-Based ML
Graphs are fundamental mathematical structures used to model pairwise relationships between objects. A graph consists of nodes (also known as vertices) that represent entities or objects, and edges (also known as links) that denote the connections or interactions between these entities. This versatile framework allows graphs to effectively capture and represent complex interdependencies and structures found in various domains, such as social networks, transportation systems, biological networks, and more. Understanding the properties and behaviors of graphs is essential for analyzing and interpreting the intricate relationships inherent in interconnected data.
Focus Areas: Knowledge Graphs and Graph Neural Networks
In this session, we will concentrate on two primary areas within the realm of graph-based data analysis:
- Knowledge Graphs
- Graph Neural Networks (GNNs)
1. Knowledge Graphs
A Knowledge Graph is a specialized type of graph that represents structured information about entities and their interrelations in a specific domain. Unlike general graphs, knowledge graphs emphasize semantic relationships and often incorporate rich metadata. Key characteristics include:
- Entities as Nodes: Represent real-world objects, concepts, or events.
- Semantic Relationships as Edges: Define the type and nature of the relationship between entities (e.g., “author_of”, “located_in”).
- Attributes: Additional information about nodes and edges, providing more context.
Use Cases of Knowledge Graphs:
- Search Engines: Enhancing search results with contextual information.
- Recommendation Systems: Suggesting products or content based on user preferences and relationships.
- Natural Language Processing: Improving understanding and generation of human language by leveraging structured knowledge.
Notebooks - Basics
2. Graph Neural Networks (GNNs)
Graph Neural Networks extend traditional neural networks to operate on graph-structured data, enabling the modeling of complex relationships and dependencies between entities. Key benefits of GNNs include:
- Relational Understanding: Capture intricate relationships and dependencies between entities in a graph.
- Scalability: Efficiently handle large-scale graphs with millions of nodes and edges.
- Flexibility: Applicable to various domains, including natural language processing, recommendation systems, and bioinformatics.
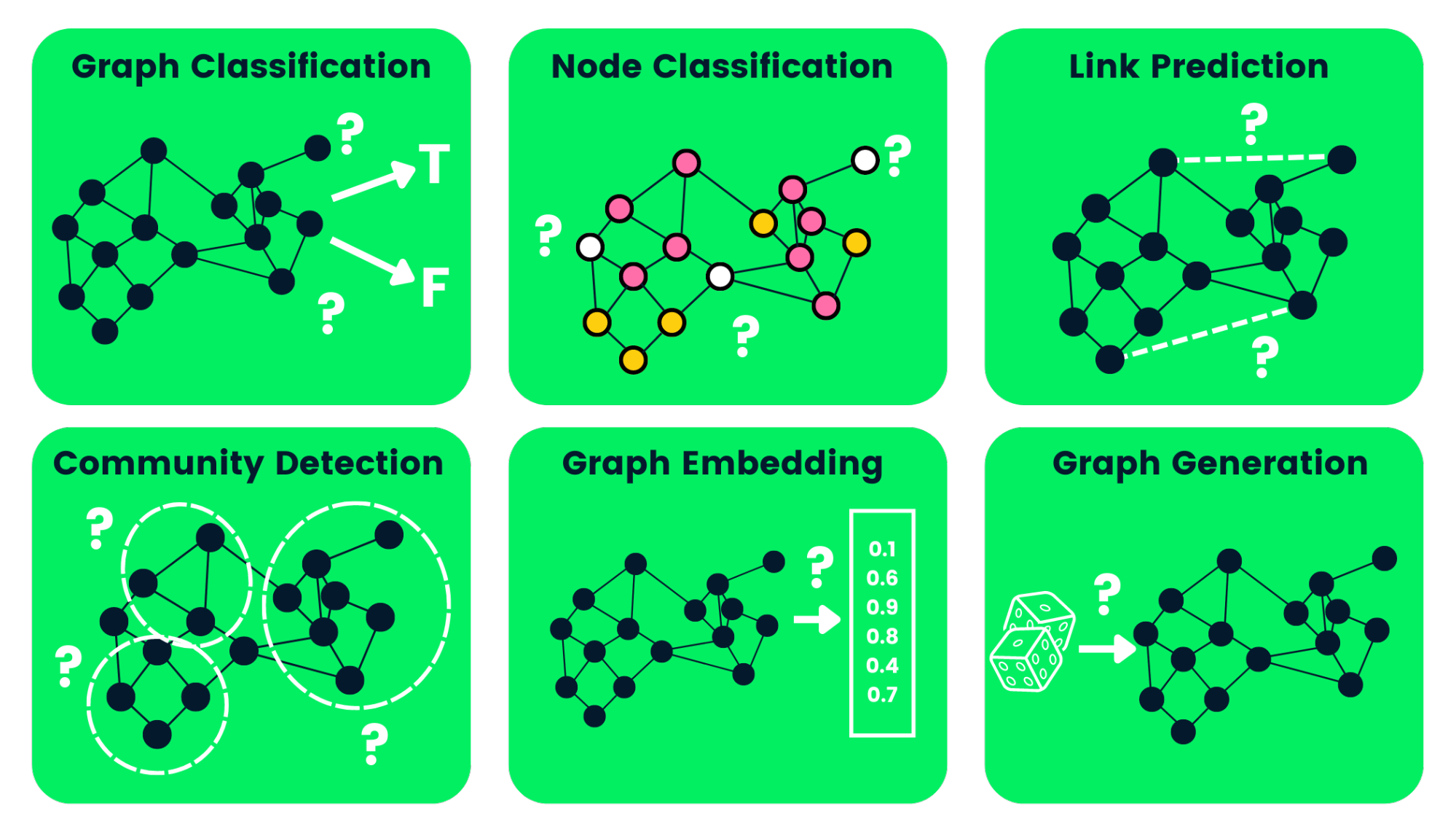
Applications of GNNs:
- Node Classification: Predicting the category or type of an entity.
- Link Prediction: Inferring missing relationships between entities.
- Graph Classification: Categorizing entire graphs based on their structure and node attributes.